Minkowski Eşitsizliği
Minkowski Eşitsizliği, sonlu sayıda, hepsi sıfır olmayan  , , 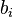 , i=1,2,...,n pozitif sayılarında, p>1 için aşağıdaki eşitsizliğe denir: , i=1,2,...,n pozitif sayılarında, p>1 için aşağıdaki eşitsizliğe denir: 
Hölder Eşitsizliğinden türetilebilen, uygulamada oldukça yararlı bu eşitsizliği Alman matematikçi Hermann Minkowski (1864-1909) elde etmiştir.
Bu sayfa normlar ile ilgili Minkowski eşitsizliği içindir. Bkz.Minkowski'nin konveks cisimler için ilk eşitsizliği için konveks geometride Minkowski eşitsizliği.
üçgen'de, Minkowski eşitsizliği' Lp uzayı normlu vektör uzayı' belirlemesidir. diyelimki S bir ölçüm uzayı olsun,ve diyelimki 1 ≤ p ≤ ∞ ve diyelimki Lp(S) ögeleri f ve g olsun. ise Lp(S) içindeki f + gdir, ve bizim üçgen eşitsizliği'miz var

için eşitliği ile 1 < p <∞ eğer ve yalnızca eğerf ve g pozitifliği doğrusal bağımlılık, yani burada bazı  ≥ 0.için f = ≥ 0.için f =  g aşağıdaki norm ile verilir: g aşağıdaki norm ile verilir:
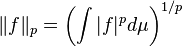
Eğer p < ∞, veya p = ∞ durumu içinde zorunlu üstünlük ile

Minkowski eşitsizliği Lp(S) içinde üçgen eşitsizliğidir,aslında bu durumun daha genel durumu var,
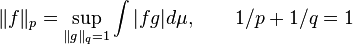
bunun sağ-el tarafta üçgen eşitsizliğinin tatmin edici olduğunu görmek kolay
Hölder eşitsizliği gibi,Minkowski eşitsizliği dizisi özelleştirilebilir ve sayarak ölçülen vektörler tarafından kullanılıyor:

için tümgerçel (veya karmaşık) x1, ..., xn, y1, ..., yn sayıları için ve burada n ;S'in kardinalite'sidir.(S'in ögelerinin sayısı).
İspatı
İlk, kanıtı f+g sonludur p-norm eğer f ve g ikilisi olarak,bunlar ile aşağıda
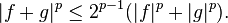
Nitekim, aslında burada  konveks üzerinde konveks üzerinde 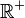 ( ( birden büyük için) ve yine, konveksite tanımı ile, birden büyük için) ve yine, konveksite tanımı ile,
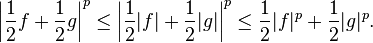
Bunun anlamı
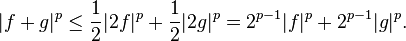
Şimdi, yasal olarak konuşabiliriz  . Sıfır ise, Minkowski eşitsizliği tutar.Şimdi varsayalım ki . Sıfır ise, Minkowski eşitsizliği tutar.Şimdi varsayalım ki  sıfır değildir.Hölder's eşitsizliği kullanılıyor. sıfır değildir.Hölder's eşitsizliği kullanılıyor.
 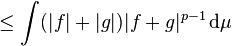   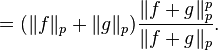
Biz elde Minkowski'nin eşitsizliği ile  her iki taraf çarparız. her iki taraf çarparız.
Minkowski İntegral Eşitsizliği
Varsayalımki (S1,μ1) ve (S2,μ2) are iki ölçüm uzayıs ve F : S1×S2 → R ölçülebilirdir. ise Minkowski's integral eşitsizliği is Stein 1970, §A.1dir, Hardy, Littlewood & Pólya 1988, Theorem 202:
![\left[\int_{S_2}\left|\int_{S_1}F(x,y)\,d\mu_1(x)\right|^pd\mu_2(y)\right]^{1/p} \le \int_{S_1}\left(\int_{S_2}|F(x,y)|^p\,d\mu_2(y)\right)^{1/p}d\mu_1(x),](http://upload.wikimedia.org/math/7/e/a/7ea2936a424748afa157ba176301e22b.png)
durumunda belirgin değişiklikler p = ∞. eğer p > 1, ve her iki taraf sonlu, ise eşitlikle örtüşür eğer |F(x,y)| = φ(x)ψ(y) a.e.bazı negatif ölçülebilir fonksiyonlar φ ve ψ için.
Eğer μ1 iki nokta kümesi sayma ölçüsüS1 = {1,2}, ise Minkowski eşitsizliği bir özel durum olarak verir: için ƒi(y) = F(i,y) yapıştırma için i = 1,2, integral eşitsizliğini verir.
![\begin{align}
\|f_1 + f_2\|_p &= \left[\int_{S_2}\left|\int_{S_1}F(x,y)\,d\mu_1(x)\right|^pd\mu_2(y)\right]^{1/p} \le\int_{S_1}\left(\int_{S_2}|F(x,y)|^p\,d\mu_2(y)\right)^{1/p}d\mu_1(x)=\|f_1\|_p + \|f_2\|_p.
\end{align}](http://upload.wikimedia.org/math/d/d/a/dda5ecb1e78cb09126074e7e0ee75bb5.png) -
- kaynak: tr.wikipedia.org
|