Her türlü ödev ve dokümanı
www.arsivbelge.com ile kolayca bulabilirsiniz! |
Araştırmalarınız için Arama Yapın:
Araştırmalarınız için Arama Yapın:
| |
Doppler Etkisi ( Doppler olayı )
www.arsivbelge.com
| Doppler Etkisi ( Doppler olayı ) dokümanıyla ilgili bilgi için yazıyı inceleyebilirsiniz. Binlerce kaynak ve araştırmanın yer aldığı www.arsivbelge.com sitemizden ücretsiz yararlanabilirsiniz. |
|
|
Doppler Etkisi ( Doppler olayı ) başlıklı doküman hakkında bilgi yazının devamında...
Ödev ve Araştırmalarınız için binlerce dokümanı www.arsivbelge.com sitesinde kolayca bulabilirsiniz. |
Doppler Etkisi ( Doppler olayı )
Doppler Etkisi ( Doppler olayı ) adını ünlü bilim insanı ve matematikçi Christian Andreas Doppler'den almakta olup kısaca dalga özelliği gösteren herhangi bir fiziksel varlığın frekans ve dalga boyu'nun hareketli (yakınlaşan veya uzaklaşan) bir gözlemci tarafından farklı zaman ve/veya konumlarda farklı algılanması olayıdır. Dalga kaynağının gözlemciye göre hareketinin yol açtığı ses ya da herhangi bir başka dalga olarak algılanmasıdır. Hareketsiz bir ses kaynağının yayınladığı dalganın sayısı belirli uzaklıktaki bir dinleyiciye olduğu gibi iletilir. Kaynak ya da dinleyici harekette ise birbirerine yaklaşırken dinleyici daha fazla dalga algılayacağından, saniyede algılanan dalga sayısı ya da frekans artar. Uzaklaşma durumunda ise frekans küçülür. Bu olay düdük çalan bir trenin yaklaşıp uzaklaşması sırasında açık biçimde gözlenebilir; trenin düdüğü, tren yaklaşırken frekansı artacağından tizleşecek, uzaklaşırken ise frekansı azalacağından pesleşecek.
Tarihçe
Doppler Etkisi ilk olarak 1842 yılında Avusturya'lı bilim insani Christian Andreas Doppler tarafından (Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels söylemi ile) matematiksel bir hipotez olarak ortaya atılmıştır. 1845 yılında Hollanda'lı fizikçi Christophorus Ballot tarafından ses dalgaları kullanılarak test edilmiş ve "ses kaynagi kendisine yakınlaşırken duyduğu frekansın yükseldiğini uzaklaşırken ise düştüğünü ispatladığını" söylemesi ile resmen onaylanmıştır. Aynı etki Ballot veya Doppler'dan bağımsız olarak 1848 yılında Fransız fizikçi Hippolyte Fizeau tarafından elektromanyetik dalgalar üzerinde de keşfedilmiştir. Bu yüzden nadiren de olsa bazı bilim çevrelerince Doppler-Fizeau Etkisi olarak da bilinir.
Matematiksel çözümleme
Doppler Etkisi konusunda bilinmesi gereken en önemli husus her ne kadar gözlemci dalga frekansının kendi hareketi ya da dalga kaynağının hareketi yüzünden değiştiğini görse de aslında frekansın sabit kaldığı gerçeğidir. Tam olarak ne olduğunu daha iyi anlamak icin şöyle bir örnek üzerinde düşünelim: Siz yerinizde ve hareketsizsiniz. Bir arkadaşınız sizden 10 metre uzakta duruyor ve size her saniyede bir elindeki tenis toplarından birini fırlatıyor. Burada arkadaşınızın topları her seferinde aynı doğru boyunca ve aynı hızda attığını varsayalım. Eğer arkadaşınız da hareketsiz ise her saniyede bir 10 metre yol kateden tenis toplarından biri size ulaşacaktır. Şimdi arkadaşınızın yine her saniyede bir top fırlattığını (yani aslında top fırlatma frekansı değişmiyor) ancak bu sefer size doğru yürümeye başladığını öngörelim. Bu durumda size ulaşan iki top arasındaki süre 1 saniyeden daha kısa olacaktır çünkü toplar her seferinde 10 metre 9 metre 8 metre şeklinde daha az mesafe katettikten sonra size ulaşacaktır. Elbette aynı etkinin zıttı arkadaşınız sizden uzaklaşırken de geçerli olacaktır. Bir başka deyişle toplar arkadaşınızın elinden her zaman saniyede bir çıktığı halde sizin ya da arkadaşınızın hareketi yüzünden size azalan ya da artan zamanlarda ulaşacaktır. Bu da doğal olarak arkadaşınızın size topu farklı zamanlarda fırlattığını düşünmenize sebep olur. Yani aslında Doppler Etkisi'nde "etkilenen" asıl fiziksel değişken dalga boyu'dur. Elbette dalga boyu ile frekans ters orantılı olduğundan gözlemciye göre dalga kaynağının frekansı da değişiyor gibi görünür.
Eğer (f0) frekansında dalga yayan hareketli bir kaynak bu yayılımı sadece kendinin ve bir gözlemcinin bulunduğu sabit bir dalga ortamında yapıyorsa o zaman bu dalga ort..... göre hareketsiz olan bir gözlemcinin göreceği frekansı (f) bulmak için:
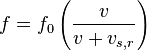
formülü kullanılır. Burada (v) dalga ortamındaki dalgaların hızı (vs r) ise kaynağın sabit olan dalga ort..... göre (eğer gözlemciye doğru hareket ediyorsa (-) eksi bir değer gözlemciden uzaklaşacak şekilde hareket ediyorsa (+) arti bir değer) hızıdır. Benzer bir analiz sabit bir dalga kaynağı ile hareketli bir gözlemci için asağıdaki gibidir. (vo) = Gözlemcinin dalga ort..... göre hızı.
Yukarıdaki örnekte de gördüğümüze benzer şekilde bu sefer gözlemcinin dalga kaynağından uzaklaşması durumunda (vo) değeri (+) arti yakinlaşması durumunda ise (-) eksi olur.
Matematiksel olarak bu iki formül elbette tek bir vektörel eşitlik olarak genelleştirilebilir. Koordinat sisteminin dalga ortamı üzerindeki herhangi bir noktanın konumunu verdiğini ve bu ortamda ses hızı'nin (c) olduğunu varsayalım ve söz konusu ortamda (s) kaynağının ( ) hızıyla hareket edip çevresine (fs) frekansında dalgalar yaydığını öngörelim. Bu dalga ortamında bir de ( ) hızıyla hareket eden bir (r) gözlemcisi olsun. Dalga kaynağı (s) ile gözlemci (r) arasındaki matematik vektörün ise (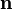 ) olduğunu öngörelim. (Yani
Bu durumda gözlemcinin algılayacağı frekans (fr):
eşitliğinden bulunabilir. Eğer  ise o zaman algılanan frekanstaki değişim daha çok dalga kaynağı ve gözlemcinin birbirine göre hızlarına bağlı olur:
Veya alternatif olarak:
Doppler'in bu analizinin ışık ışınları için de geçerli olabilmesi için yapılan ilk çalışma Hippolyte Fizeau tarafından yürütülmüştür. Ancak ışık A noktasından B noktasına gidebilmek için belli bir dalga ort..... gerek duymaz (örneğin sonsuz boşluk olan uzayda kolayca yol alır) ve Doppler Etkisi'nin ışık ışınlarına nasıl doğru bir şekilde uygulanabileceğinin anlaşılabilmesi için Einstein'in Özel Görelilik (izafiyet) teorisinin kullanımına ihtiyaç vardır.
Doppler Olayının Kullanımı
Doppler olayı, radyo, radar ve ışık dalgalarında da gözlenir. Teknikte harekette olan bir cismin hızını ölçmekte bu olaydan yararlanılır. Örneğin iyonosferde elektrik yüklü tabakaların hareketi, radyo sinyallerinin frekansındaki Doppler kaymasıyla belirlenir. İkinci Dünya Savaşı sırasında geliştirilen radarlar, yaklaşan uçakların hızlarını Doppler ilkesi aracılığıyla ölçebildiler. Doppler olayının astronomide de büyük önemi vardır. Güneş vb ışık kaynağı olan gökcisimlerinin tayfları hidrojen, helyum, demir vb elementleri belirli dalga boylarındaki soğurma ya da salma çizgilerini içerir. Gökcismi harekette ise Doppler olayı nedeniyle bu çizgilerin frekansında ve dalga boylarında laboratuvar değerlerine göre oluşan kayma küçük dalgaboyu olan mor yana doğruysa gök cismi yaklaşıyor, büyük dalga boyu olan kırmızı yana doğruysa uzaklaşıyor demektir.
Doppler ilkesinin verdiği dalga boyunun kayma miktarının dalga boyuna oranının, gökcismin hızının ışık hızına oranına eşit olacağı biçimindeki bağıntıdan gökcisminin dünyaya olan dikine hızını hesaplamak olasıdır. 1929′ da ABD’li gökbilimci Edwin Hubble’ın Mount Wilson Gözlemevi’nde galaksilerin tayflarında gözlediği kırmızıya kaymanın o kadar fazla olduğunu gözleyerek galaksilerin uzaklaşma hızlarının uzaklıkla orantılı biçimde arttığını buldu. Bu yöntem, gökcisimlerinin uzaklıklarının belirlenmesinde kullanılır.
|
Ekleyen:Ümit SERT
Kaynak:(Alıntıdır)
| Aradığınız Dokümanı Bulamadıysanız, Farklı Araştırmalar Yapmak İstiyorsanız Site İçi Arama Yapabilirsiniz! |
Ödev ve Araştırmalarınız için www.arsivbelge.com Sitesinde Kaynak Arayın: |
|
|
Ödev ve Araştırmalarınız için Arama Yapın:
|
