Poisson Dağılımı Hakkında

Araştırma ve ödevleriniz için her türlü kaynağı ve dokümanı En Geniş Araştırma ve Ödev Sitesi: www.arsivbelge.com ile bulabilir ve İsterseniz siz de kendi belge ve çalışmalarınızı gönderebilirsiniz!

Her türlü ödev ve dokümanı
www.arsivbelge.com ile kolayca bulabilirsiniz!

Araştırmalarınız için Arama Yapın:

Araştırmalarınız için Arama Yapın:

Poisson Dağılımı Hakkında
www.arsivbelge.com

Poisson Dağılımı Hakkında dokümanıyla ilgili bilgi için yazıyı inceleyebilirsiniz. Binlerce kaynak ve araştırmanın yer aldığı www.arsivbelge.com sitemizden ücretsiz yararlanabilirsiniz.

Poisson Dağılımı Hakkında başlıklı doküman hakkında bilgi yazının devamında...
Ödev ve Araştırmalarınız için binlerce dokümanı www.arsivbelge.com sitesinde kolayca bulabilirsiniz.

Poisson Dağılımı Hakkında

Poisson dağılımı, (okunuşu: puason dağılımı) olasılık kuramı ve istatistik bilim kollarında bir ayrık olasılık dağılımı olup belli bir sabit zaman birim aralığında meydana gelme sayısının olasığını ifade eder. Bu zaman aralığında ortalama olay meydana gelme sayısının bilindiği ve herhangi bir olayla onu hemen takip eden olay arasındaki zaman farkının, önceki zaman farklarından bağımsız oluştuğu kabul edilir.

Poisson dağılımı çok kere belirli sabit zaman aralığı birimleri bulunan problemlere uygulanmakla beraber, diğer birimsel aralıklı problemlere de (yani birim uzaklık, alan veya hacim içeren problemlere de) başarı ile uygulanabilir.

Tarihçe

Bu dağılım ilk defa Siméon-Denis Poisson (1781–1840) tarafından diğer olasılık hakkındaki yazıları ile birlikte 1838'de yayınlanan Recherches sur la probabilité des jugements en matières criminelles et matière civile ("Ceza hukuku ve medeni hukuk alanlarındaki hükümlerin olasılığı üzerinde araştırmalar") adındaki eserinde ortaya atılmıştır.

Örnekler

Poisson dağılımı Poisson süreci ile birlikte ortaya çıkar. Poisson süreci aralıklı karakterde olan (yani 0, 1, 2, 3 .. kere meydana çıkan) bazı olgularin bir birim zaman, alan, mekân veya hacimde sabit bir olasılıkla oluşması şekilini alır. Bu çeşit olaylara ve Poisson dağılımının uygulanmasına örnekler şunlardır:

Prusya süvari birliklerinde her bir yıl at ve katır tepmeleri ile ölen asker sayısı: Bu klasik örnek 1868'de Ladislaus Josephovich Bortkiewicz tarafından bir kitapta yayınlanmış ve çok tanınmış bir örnek olarak yıllarca askeri ve sivil yüksek okul öğrencilerine verilmiştir.
Bir saat aralığında belli bir Internet sitesine gelen bağlantılar sayısı;
Yarım saat içinde bir nakliyat deposuna yükleme-boşatılma için gelen kamyon sayısı;
Her bir beş dakika içinde bir telefon cevap merkezine gelen telefonlar sayısı;
Belli bir trafik kavşağından 1 dakika içinde geçen otomobil sayısı;
Belli bir zaman aralığında bir büyük binada yanıp çalışması duran florasan lambalarının sayısı;
Bir mucit kişinin çalışma hayatı boyunca patentini aldığı keşifler sayısı;

[Not: Birbirini takip eden Poisson tipi olaylar arasındaki aralık karşılıklı ilişkili olarak bir üstel dağılımolur. Örneğin, bir florans ampülünun çalışma süresi veya otobüslerin gelmesi arasındaki bekleme zamanı.]

Poisson dağılımının genel odaklandığı rassal değişken bir sayılabilen olaydır; bu olay belli bir sabit uzunlukta olan (genellikle zaman) aralıkta ayrık olarak ortaya çıkar ve bu aralıkta gözlenen olayların sayısı Poisson dağılım için rassal değişkendir. Bu sabit aralıkta ortaya çıkan olaylar sayısının beklenen değeri (ortaya çıkmanın ortalama sayısı) λ olarak sabittir ve bu ortalama değer aralık uzunluğuna orantılıdır. Eğer her 4 dakikalık zaman aralığı içinde ortalama 5 olay meydana geliyorsa, sabit 8 dakikalık aralıkta ortalama 10 (=8x5/4) olay ortaya çıkar. Herhangi bir negatif olmayan bir tamsayı olan k sayıda (k = 0, 1, 2, 3...) olay ortaya çıkma olasılığı şöyle ifade edilir:

f(k, \lambda)=\frac{\lambda^k e^{-\lambda}}{k!},\,\!

burada

e, doğal logaritmanın tabanı (e = 2.71828...);
k, olasılığı fonksiyon ile verilmekte olan olayın ortaya çıkma sayısı;
k!, k için faktöriyel
λ verilen sabit aralıkta ortaya çıkma sayısının beklenen değeri; bir pozitif gerçel sayı.

Bu k'nin fonksiyonu Poisson dağılım için olasılık kütle fonksiyonu olur.

Poisson dağılımı için λ parametresi yalnızca beklenen değer, yani ortaya çıkan 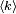$\scriptstyle\langle k \rangle$ sayıda olay için bir ortalama, değildir. Aynı zamanda

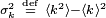
\scriptstyle\sigma_k^2 \ \stackrel{\mathrm{def}}{=}\ \langle k^{2} \rangle - \langle k \rangle^{2}

yani varyans da olur. Böylece gözlenen olay meydan çıkış sayısı bir ortalama değer λ ile bir standart sapması 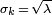$\scriptstyle\sigma_{k}\, =\, \sqrt{\lambda}$ olması niteliklerini taşiyan bir olasılık dağılımı, Poisson dağılımı, göstermektedir.

Genellikle bir Poisson dağılımı büyük sayıda olay ortaya çıkabilmesi mümkün olduğu, ama bu ortaya çıkması mümkün olayların nadir olduğu kabul edilen, sistemlerde uygulanabilir. Bilimsel alanlarda klasik örnekler atomların nükleer parçalanması; verilen bir DNA zincirinde ortaya çıkan mutasyon sayısı vb. Bu örneklerle ve diğer birçok örneğin için, ortaya çıkan nadir olay sayısı ayrık denemelerin sonucudur ve daha kesinlikle bir binom dağılım kullanılarak model haline getirebilinirler. Fakat n ve λ/n parametreli bir binom dağılımı (yani her deneme için λ/n başarı olasılığı olan n sayıda deneme için belirli bir başarı sayısı için olasılık dağılımı), deneme sayısı n büyüyüp limitte sonsuzluğa yaklaştıkça, beklenen değeri λ olan bir Poisson dağılıma yakınsalaşır. Bu limit bazan nadir olaylar kuralı olarak anılmaktadır. Bu ifade bir bakıma yanıltıcıdır; çünkü birçok Poisson dağılımı ile modellenebilen olaylar arasında birçoğu (örneğin bir otobüs durağına yarım saat aralığında gelen otobüs sayısı; bir mobil telefona bir saat aralığında gelen çağrı sayısı gibi) hiç de nadir olmayan olaylar bulunur. Ancak binom dağılımının büyük sayılar için hesaplanması faktöriyel sayılar kullanılması gerektirdiği için, bu uzun hesaplama biraz sıkıcı görülebilmekte ve bu nedenle Poisson dağılımı yaklaşık olarak binom dağılım yerine kullanılmaktadır.

Binom dağılımından limitte Poisson dağılım olasılık kütle fonksiyonunun çıkartılmasınin matemetiksel kanıtı şöyle yapılır:

Önce, değişkenler hesabı (calculus) içinde kullanılan limitin şöyle ifade edildiğı hatırlanır:

\lim_{n\to\infty}\left(1-{\lambda \over n}\right)^n=e^{-\lambda}.

p = λ/n eşitliği bu ifade içine konulursa, şu genel denkleme varılır:

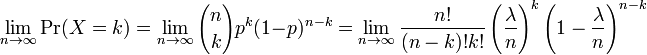
\lim_{n\to\infty} \Pr(X=k)=\lim_{n\to\infty}{n \choose k} p^k (1-p)^{n-k} =\lim_{n\to\infty}{n! \over (n-k)!k!} \left({\lambda \over n}\right)^k \left(1-{\lambda\over n}\right)^{n-k}

Şimdi bu son ifade biraz daha açılır ve şu elde edilir:

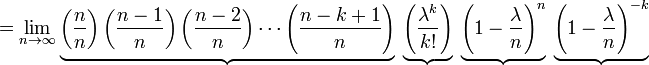
=\lim_{n\to\infty} \underbrace{\left({n \over n}\right)\left({n-1 \over n}\right)\left({n-2 \over n}\right) \cdots \left({n-k+1 \over n}\right)}\ \underbrace{\left({\lambda^k \over k!}\right)}\ \underbrace{\left(1-{\lambda \over n}\right)^n}\ \underbrace{\left(1-{\lambda \over n}\right)^{-k}}

Limitte, ilk parantez içindeki ifade 1 e yakınsama gösterir (yani n ∞'a yaklaştıkça, ilk parantezdeki ifade 1'e yakınsar ) ve ikinci parantez içindeki ifade, ifade içinde n olmaması nedeniyle, sabit kalır; üçüncü parantez içindeki ifade e^−λ değerine yakınsar ve son olarak da dördüncü parantezdeki ifade, 1 e yakınsar. Sonuçta, limitte şu ortaya çıkar:

{\lambda^k e^{-\lambda} \over k!}.\,\!

Daha genel olarak, n ve p_n parametreleri olan binom rassal değişkenler için bir sıra Binom ifadesi

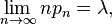
\lim_{n\rightarrow\infty} np_n = \lambda,

olursa, bu seri dağılımda ortalaması λ olan bir Poisson rassal değişkeni için serilere yakınlaşır.^[1].

Özellikler

Poisson dağılımı gösteren rassal bir değişken için beklenen değer ve varyans değeri de λdır. Poisson dağılımının yüksek momentleri λ terimleri ile oluşan (matematiksel kombinatorik kuramında anlamlı olan katsayıları bulunan) Touchard polinomlarıdır. Eğer Poisson dağılımı için beklenen değer 1 ise, o zaman Dobinski'nin formülüne göre ninci moment n büyüklüğünde olan set bölünümlerinin sayısına eşittir.

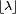Tam sayılı olmayan bir λ lambda parametreli Poisson dağılımı gösteren bir rassal değişkenin mod değeri, λ 'dan küçük olan en büyük pozitif tamsayıya, yani $\scriptstyle\lfloor \lambda \rfloor$ 'ya, eşittir.

Poisson dağılımı gösteren rassal değişkenlerin toplamı:

Eğer

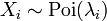X_i \sim \mathrm{Poi}(\lambda_i)\,

ifadesi

\lambda_i

parametresi ile Poisson dağılımı gösteriyor ve

X_i

terimleri bağımsız iseler, o halde

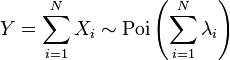
Y = \sum_{i=1}^N X_i \sim \mathrm{Poi}\left(\sum_{i=1}^N \lambda_i\right)\,

ifadesi de parametresi toplama katılan parametre toplamlarından olan bir Poisson dağılımı gösterir.

Beklenen değeri λ olan Poisson dağılımınin moment üreten fonksiyonu şu ifade ile verilir:

\mathrm{E}\left(e^{tX}\right)=\sum_{k=0}^\infty e^{tk} f(k;\lambda)=\sum_{k=0}^\infty e^{tk} {\lambda^k e^{-\lambda} \over k!} =e^{\lambda(e^t-1)}.

Poisson dağılımı için tüm kümülantlar beklenen değer olan λya eşittirler. Poisson dağılımı için ninci faktöriyel moment λⁿ olur

Poisson dağılımlari sonsuz olarak bölünebilir olasılık dağılımlarıdır.

Poi(λ₀) ile Poi(λ) arasındaki yönlendirilmiş Kullback-Leibler ayrılımı şöyle ifade edilir;

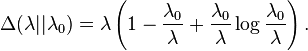\Delta(\lambda||\lambda_0) = \lambda \left( 1 - \frac{\lambda_0}{\lambda} + \frac{\lambda_0}{\lambda} \log \frac{\lambda_0}{\lambda} \right).

kaynak: tr.wikipedia.org

Ekleyen:Ümit SERT
Kaynak:(Alıntıdır)

Aradığınız Dokümanı Bulamadıysanız, Farklı Araştırmalar Yapmak İstiyorsanız Site İçi Arama Yapabilirsiniz!
Ödev ve Araştırmalarınız için www.arsivbelge.com Sitesinde Kaynak Arayın:

Ödev ve Araştırmalarınız için Arama Yapın:


	Benzer Dokümanları İnceleyin İnsan Irkı ve İnsan Türünün Dağılımı(5387) Gelir Dağılımı Analizi(5365) Burr Dağılımı ile Rüzgar Enerjisi Potansiyeli Tahmini(5362)

Tanıtım Yazıları

Türkçe İtalyanca ve Almanca Cümle Çevirisi İçin Birimçevir Sitesi

Esenyurt, Beylikdüzü ve Kartal Bölgelerinde Satılık Daire İlanları

Belge Çevirisi

Siz de Tanıtım Yazısı Yayınlamak İçin Tıklayın

Diğer Dökümanlarımızı görmek için: www.arsivbelge.com tıklayın.
Siz de Yorum Yapmak İstiyorsanız Sayfanın Altındaki Formu Kullanarak Yorum Yazabilirsiniz!

Yorum Yaz

Yorumunuz site yönetimi tarafından onaylandıktan sonra yayınlanacaktır!