Babil ve Mısırda Matematik

Matematiğin kökeninin sayma kavramına dayandığı düşünülüyor. Tarihi boyunca insanoğlu zaman, mesafe ve çeşitli büyüklükleri ölçme, kaydetme ve paylaşma ihtiyacıyla yüzleşmiş, bu amaçla çeşitli yöntemler geliştirmiştir. Günümüze kadar ulaşabilen kalıntılardan anlaşıldığı kadarıyla insanoğlunun M.Ö.35.000 yılından itibaren büyüklükleri sayıp kaydedebildiğini biliyoruz. Muhtemelen günümüze ulaşan en eski matematiksel nesne, yaklaşık olarak M.Ö.35.000 yılına ait olduğu düşünülen, Swaziland’ın Lebombo dağındaki Border Mağarasında bulunan Lebombo Kemiğidir. Bu; üzerinde 29 ayrı çentik bulunan bir maymun kaval kemiğidir. Üzerindeki çentiklerin sayısından, bunun bir çeşit ay takvimi veya menstrüel takvim olabileceği düşünülüyor. Ayrıca yaklaşık olarak M.Ö.30.000 yıllarında paleolitik dönem (Yontma taş devri, M.Ö.600.000-10.000) insanları Orta Avrupa ve Fransa’da çeşitli kemikler üzerinde çentikler atarak tarih kayıtları yapmışlardır.

Tarihöncesine ait bir matematiksel nesne olduğuna inanılan en heyecan verici kalıntı ise, Belçikalı jeolog Jean de Heinzelin de Braucourt’ un 1960 yılında Afrika’nın, Nil nehri ve Edward gölü yakınlarında konumlanan İshango Bölgesinde –günümüzde Uganda-Kongo sınırında bulunmaktadır- bulduğu İshango Kemikleridir. İshango kemikleri de öncekiler gibi maymun kemiği üzerine çentikler atılarak oluşturulmuş bir matematik gerecidir. Tahmini olarak M.Ö.20.000 veya biraz daha eski bir döneme ait olduğu düşünülüyor

İshango kemiklerinin üzerindeki çentikler, öncekilerden farklı olarak, belli bir düzene sahip gibi görünüyor. Bu düzenin matematiksel bir anlamı olabileceği düşünülüyor, diğer yandan bu çentiklerin rastgele olabileceği, kemikleri rahat kavramak ve tutmak için çizilmiş olabileceği de zayıf bir ihtimal olarak eldedir.

Çentiklerin düzenine kısaca değinecek olursak, kemikler uzunluğu boyunca 3 sütuna ayrılıp, her sütuna değişik sayılarda çentikler gruplar halinde atılarak bir sayı dizisioluşturulmuştur.  Kemiklerin orta sütunlarındaki çentik sayıları 3, 6, 10, 5, 7 şeklinde dizilmiştir. Dikkat edilirse (3-6), (10-5) şeklinde grupların olduğu görülür. Bu yüzden birçok bilim adamı bu kemiklerin o dönemde bazı basit hesaplarda, iki ile çarpma veiki ile bölme işlemlerinde kullanılan bir araç olduğunu düşünüyor.

Sağ ve sol sütunlarda ise çentiklerin tamamı tek sayıları belirtmektedir. Dahası, her nasılsa, sol sütundaki çentikler 10 ile 20 arasındaki asal sayıları (11, 13, 17, 19), sağ sütundaki çentikler ise 10 ve 20 sayılarının birer fazlası ve eksiği olan sayıları (9, 19, 21, 11) belirtmektedirler.

Asal sayı kavramının, M.Ö.10.000 den sonra ortaya çıkan bölme kavramından önce insanoğlunun gündemine gelmesi olası bir durum olarak görülmemekte, bu nedenle kemiklerin asal sayılarla ilgili olduğu düşünülmemektedir. Diğer yandan, dikkat edilirse kemiklerdeki çentik toplamı orta sütunda 48, sağ ve sol sütunlarda ise 60 dır. Bu nedenle kemiklerin 6 aylık bir ay takvimi veya bir çeşitmenstrüel takvim olabileceği de düşünülmektedir. Günümüzde İshango kemikleri Belçika’da Brüksel’de bulunan Riyal Belgian Institute of Natural Sciences de sergilenmektedir.

İnsanoğlu çok daha eski çağlardan beri çeşitli çizimler yapmaktaydı fakat bunların geometrik anlamı oldukarı düşünülmüyordu, daha çok gördükleri hayvanları vs çiziyorlardı. Ama bu karanlık çağdan günümüze ulaşan kalıntılardan, en erken geometrik çizimlerin M.Ö.25.000 yıllarında yapıldığı düşünülüyor.

M.Ö.5.000 li yıllardan itibaren Babil ve Mısır Uygarlıklarının etkisiyle önemli matematiksel gelişmeler meydana gelmiştir. Babilliler dediğimiz toplum, Sümerlilerin ilk zamanlarından (M.Ö.5.000) başlayıp M.Ö.500 e kadar uzanan bir zaman dilimindeMezopotamya dediğimiz bölgede yaşayan topluluktur.

Bu dönemdeki matematik de, önceki çağlardaki gibi tamamen günlük ihtiyaçların giderilmesi amacını taşıyordu. Arazilerin alanlarının veya sınırlarının hesaplanması gibi. Örneğin eski Mısır’da Nil Nehrinin her yıl taştığı ve tarlaların sınırlarının kaybolduğu, bunun üzerine insanların her yıl bu sınırları tekrar saptayıp tarlaları paylaştıkları, bu amaçla da bazı geometrik yöntemler geliştirdikleri söylenir.

M.Ö.4.000 de Babil ve Mısır da bir çeşit takvim kullanılmaya başlanmış, M.Ö.3.400de sadece basit

çizgilerden oluşan birtakım semboller sayılar yerine kullanılmıştır.M.Ö.3.000 de Ortadoğu ve Akdeniz civarında ilk abaküs geliştirilmiş, yine M.Ö.3.000 yıllarında Mısırlılar okunaksız şekillerden oluşan birnumara sistemini kullanmaya başlamışlardır. Bu rakamlar onluk sistem için geliştirilmiştir. Aşağıdaki şekilde bu rakamları ve bu sistemde yazılmış bazı örnek sayılar var.

Aynı dönemde Babilliler de, finansal işlemleri kayıt altına almak amacıyla 60 tabanında bir sayı sitemi geliştirip buna uygun rakamlar kurmuşlardır. Bu sistemdesıfır sayısı olmadığı için finansal işlemler için geliştirildiği düşünülmektedir. Aşağıdaki şekilde bu rakamları ve bir örnek sayı verilmiştir.( )

M.Ö.1900 de Mısır’da ise günümüzde sahip olduğumuz en eski yazılı matematik metni olan Moscow Papirus yazılmıştır. M.Ö.1.850-1.700 yıllarında ise Mısır’daRhind papirus ve Babil’de Plimpton 322 (tablet) metinleri yazılmıştır. Bu üç belge, matematik tarihinin ilk yazılı belgeleridir. Bu üç belge de günlük matematik problemleri ile alakalı olup, belgelerde ağırlıklı olarak geometrik problemler üzerinde durulmuştur.

Rhind Papirus, Ahmes tarafından yazılmıştır, 6 metre uzunluğunda ve 33 santim genişliğinde bir rulodur. İngiliz bilgini A. Hanry Rhind tarafından Mısır’dan satın alınıp British Museum’a taşınmıştır. Bugün elimizde olan bu belgenin aslında M.Ö.1.650 de yazıldığı fakat bunun Ahmes’in 200 yıl öncesinin bir metninin kopyalaması olduğu biliniyor. Rhind papirusunun içeriğinde 85 adet problem ve çözümleri bulunmaktadır.

Moscow papirusu ise Mısırbilimci (egyptologist) Vladimir Golenishchev tarafından 1892 de Mısır’da satın alınmıştır. Bugün Moskova’da Pushkin State Museum of Fine Arts da sergilenmektedir. İçerisinde 25 adet problem ve çözümleri vardır.

Plimpton 322 tableti ise Columbia Üniversitesinde G.A. Plimpton koleksiyonunda bulunan 322 numaralı tablettir. Pisagor üçlüsü problemi üzerinde durulmuştur tablette. (Pisagor üçlüsü; 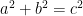 olacak şekilde (a,b,c) üçlüleri bulma problemidir).

Ayrıca günümüzde bundan başka 300 civarında Babil tableti vardır, bunların okunma çalışmaları çeşitli müzelerde halen devam etmektedir. Örneğin British Museum’da bulunan bir Babil tabletinin bir çevirisi aşağıdaki gibidir,

Uzunluk 4 ve köşegen 5. O zaman genişlik kaç?

Ölçüsü bilinmiyor.

4 kere 4, 16 eder.

5 kere 5, 25 eder.

25 ten 16 çıkarırsan 9 kalır.

9 elde etmek için kaç kere kaç almalıyım?

3 kere 3, 9 eder.

Genişlik 3.

Plimton 322 tabletinde toplam 15 adet Pisagor üçlüsü bulunmaktadır ve içlerinde  (13500, 12709, 18541) gibi büyük üçlüler de vardır. Pisagor teoremi olarak bilinen kuralın, Pisagor’dan çok önceden beri Babillilerde kullanılıyor olduğu, Plimpton 322 ve diğer Babil tabletleri sayesinde günümüzde kabul görmektedir.

Plimpton 322 de başka konular da ele alınmıştır. Örneğin 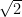 sayısının yaklaşık değeri için:

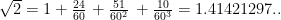
formülü kullanılarak virgülden sonra 5 basamakla yaklaşılmıştır.

Bu dönemlerde Babil ve Mısır uygarlıkları dışında Çin’de de matematiksel gelişmeler kaydedilmiştir. Örneğin M.Ö.1.400 yıllarında da Çin’de sıfırı olmayan bir sayı sistemi kullanılmaya başlanmıştır. Aşağıda bu sistemdeki numaralar verilmiştir.

M.Ö. 575 yılında ise Thales Babillilerin matematik bilgilerini Yunanistan’a taşıdı. Bu bilgileri kullanarak geometrinin temelini attı. M.Ö.530 yıllarında da Pisagor Croton’a (İtalya’da) giderek orada halka felsefe, matematik, müzik ve reenkarnasyon eğitimi vermeye başladı. Eski Mısır ve Babil’deki matematik bilgileri Antik Yunan’a taşınmasından sonra matematik büyük bir atılım gerçekleştirmiştir.

Bu yazımı burada sonlandırıyorum, matematik tarihi üzerine yazılarım kronolojik olarak devam edecek. Bir sonraki yazım Antik Yunan matematiği üzerine olacak.

 kaynak: sahmath.com

teşekkürler güzel yazı olmuş ancak bir de slayt ekleseydik ve birazda basit yazmış olsak daha iyi olabilirdi.